Advertisements
Advertisements
प्रश्न
In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that:
4(BL2 + CM2) = 5 BC2
Advertisements
उत्तर
Given: Δ ABC right angled at A, i.e., A = 90, where BL and CM are the medians.
To Prove: 4(BL2 + CM2) = 5BC2
Proof:
Since BL is the median,
AL = CL = `1/2` AC ...(1)
Similarly, CM is the median
AM = MB = `1/2`AB ...(2)
∴ by Pythagoras theorem,
(Hypotenuse)2 = (Height)2 + (Base)2 ...(3)
In ΔBAC,
(BC)2 = (AB)2 + (AC)2 ...(4)
∠BAC = 90°
In ΔBAL,
(BL)2 = AB2 + AL2 ...(From 1)
BL2 = AB2 + `(("AC")/2)^2`
BL2 = AB2 + `("AC"^2/4)`
Multiply both sides by 4,
4BL2 = 4AB2 + AC2 ...(5)
In ΔMAC,
CM2 = AM2 + AC2 ...(From 2)
CM2 = `(("AB")/2)^2` + AC2
CM2 = `("AB")^2/4` + AC2
Multiply both sides by 4,
4CM2 = AB2 + 4AC2 ...(6)
Adding 5 and 6,
4BL2 + 4CM2 = (4AB2 + AC2) + (AB2 + 4AC2)
4(BL2 + CM2) = 5AB2 + 5AC2
∴ 4(BL2 + CM2) = 5BC2
Hence, proved.
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
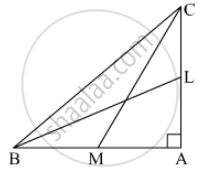
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height
Find the distance between the helicopter and the ship
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is __________
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
