Advertisements
Advertisements
प्रश्न
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
उत्तर

It is given that, Pranali and Prasad have same speed.
Thus, they cover same distance in 2 hours.
i.e. OA = OB
Let the speed be x km per hour.
According to Pythagoras theorem,
In ∆AOB
\[{AB}^2 = {AO}^2 + {OB}^2 \]
\[ \Rightarrow \left( 15\sqrt{2} \right)^2 = {AO}^2 + {OA}^2 \]
\[ \Rightarrow 450 = 2 {AO}^2 \]
\[ \Rightarrow {AO}^2 = \frac{450}{2}\]
\[ \Rightarrow {AO}^2 = 225\]
\[ \Rightarrow AO = 15 km\]
\[ \Rightarrow BO = 15 km\]
\[\text{Speed} = \frac{Distance}{Time}\]
\[ = \frac{15}{2}\]
\[ = 7 . 5 \text{km per hour}\]
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Identify, with reason, if the following is a Pythagorean triplet.
(11, 60, 61)
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
Find the Pythagorean triplet from among the following set of numbers.
2, 6, 7
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12 cm, SM = 8 cm, find CS
Find the length of the support cable required to support the tower with the floor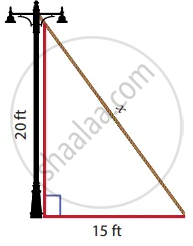
Two angles are said to be ______, if they have equal measures.
