Advertisements
Advertisements
प्रश्न
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
उत्तर
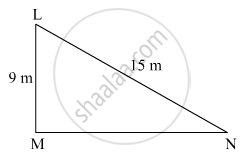
Let LN be the ladder of length 15 m that is resting against a wall. Let M be the base of the wall and L be the position of the window.
The window is 9 m above the ground. Now, MN is the distance between the base of the wall and that of the ladder.
In the right-angled triangle LMN, ∠M = 90°. Hence, side LN is the hypotenuse.
According to Pythagoras' theorem,
l(LN)2 = l(MN)2 + l(LM)2
⇒ (15)2 = l(MN)2 + (9)2
⇒ 225 = l(MN)2 + 81
⇒ l(MN)2 = 225 − 81
⇒ l(MN)2 = 144
⇒ l(MN)2 = (12)2
⇒ l(MN) = 12
∴ Length of seg MN = 12 m.
Hence, the distance between the base of the wall and that of the ladder is 12 m.
संबंधित प्रश्न
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
Find the Pythagorean triplet from among the following set of numbers.
3, 4, 5
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
From given figure, In ∆ABC, If AC = 12 cm. then AB =?

Activity: From given figure, In ∆ABC, ∠ABC = 90°, ∠ACB = 30°
∴ ∠BAC = `square`
∴ ∆ABC is 30° – 60° – 90° triangle
∴ In ∆ABC by property of 30° – 60° – 90° triangle.
∴ AB = `1/2` AC and `square` = `sqrt(3)/2` AC
∴ `square` = `1/2 xx 12` and BC = `sqrt(3)/2 xx 12`
∴ `square` = 6 and BC = `6sqrt(3)`
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
Two squares having same perimeter are congruent.
