Advertisements
Advertisements
प्रश्न
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
उत्तर
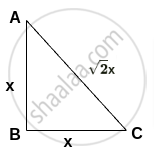
Let, the sides of the triangle be, x: `sqrt2`x and x.
AB2 + BC2 = x2 +x2 = 2x2
AC2 = `(sqrt2 x)^2` = 2x2
AB2 + BC2 = AC2
Conversely, if in any triangle, the square on the largest side of the triangle is equal to the sum of the squares on remaining two sides, then the triangle is a right-angled triangle and the angle opposite to the largest side is a right-angle.
Therefore, Δ ABC is a right-angled triangle.
APPEARS IN
संबंधित प्रश्न
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
Sides of triangles are given below. Determine it is a right triangles? In case of a right triangle, write the length of its hypotenuse. 3 cm, 8 cm, 6 cm
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)

In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
Find the length of diagonal of the square whose side is 8 cm.
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
Find the Pythagorean triplet from among the following set of numbers.
4, 5, 6
A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
