Advertisements
Advertisements
प्रश्न
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
उत्तर
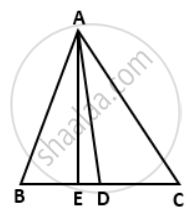
We have ∠AED = 90°
∴ ∠ADE < 90° and ∠ADC > 90°
i.e. ∠ADE is acute and ∠ADC is obtuse.
In ΔABD, ∠ADE is an acute angle.
∴ AB2 = AD2 + BD2 - 2 x BD x DE
⇒ AB2 = AD2 + `(1/2"BC")^2 - 2 xx (1)/(2)"BC" xx "DE"`
⇒ AB2 = AD2 + `(1)/(4)"BC"^2 - "BC" xx "DE"`
⇒ AB2 = AD2 + BC x DE - `(1)/(4)"BC"^2`. ....(ii)
APPEARS IN
संबंधित प्रश्न
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)

Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm;
find the length of side BC.
In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
Find the length of diagonal of the square whose side is 8 cm.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 60, 61
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
In the given figure. PQ = PS, P =R = 90°. RS = 20 cm and QR = 21 cm. Find the length of PQ correct to two decimal places.
Find the unknown side in the following triangles
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height
Two rectangles are congruent, if they have same ______ and ______.
In a triangle, sum of squares of two sides is equal to the square of the third side.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
