Question

In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1

Answer 1

Correct answer: C

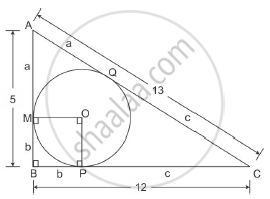
It is given that AB = 5 and BC = 12
Using Pythagoras theorem

AC²=AB²+BC²

5²+12²

=169

Thus AC = 13
We know that two tangents drawn to a circle from the same point that is exterior to the circle are of equal lengths.

Thus AM = AQ = a
Similarly MB = BP = b and PC = CQ = c
We know
AB = a + b = 5
BC = b + c = 12 and
AC = a + c = 13

Solving simultaneously we get a=3, b=2 and c=10
We also know that the tangent is perpendicular to the radius 
Thus OMBP is a square with side b
Hence the length of the radius of the circle inscribed in the right angled triangle is 2 cm.