Advertisements
Advertisements
Question
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
Solution
Correct answer: C
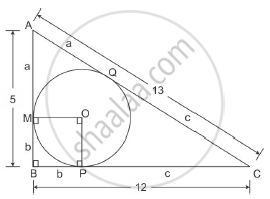
It is given that AB = 5 and BC = 12
Using Pythagoras theorem
AC2=AB2+BC2
52+122
=169
Thus AC = 13
We know that two tangents drawn to a circle from the same point that is exterior to the circle are of equal lengths.
Thus AM = AQ = a
Similarly MB = BP = b and PC = CQ = c
We know
AB = a + b = 5
BC = b + c = 12 and
AC = a + c = 13
Solving simultaneously we get a=3, b=2 and c=10
We also know that the tangent is perpendicular to the radius
Thus OMBP is a square with side b
Hence the length of the radius of the circle inscribed in the right angled triangle is 2 cm.
APPEARS IN
RELATED QUESTIONS
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Identify, with reason, if the following is a Pythagorean triplet.
(24, 70, 74)
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9AQ2 = 9AC2 + 4BC2
