Advertisements
Advertisements
प्रश्न
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
उत्तर
Correct answer: C
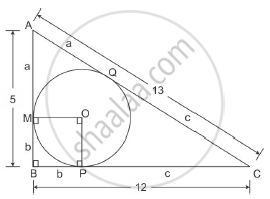
It is given that AB = 5 and BC = 12
Using Pythagoras theorem
AC2=AB2+BC2
52+122
=169
Thus AC = 13
We know that two tangents drawn to a circle from the same point that is exterior to the circle are of equal lengths.
Thus AM = AQ = a
Similarly MB = BP = b and PC = CQ = c
We know
AB = a + b = 5
BC = b + c = 12 and
AC = a + c = 13
Solving simultaneously we get a=3, b=2 and c=10
We also know that the tangent is perpendicular to the radius
Thus OMBP is a square with side b
Hence the length of the radius of the circle inscribed in the right angled triangle is 2 cm.
APPEARS IN
संबंधित प्रश्न
In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
In the figure below, find the value of 'x'.

Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
Find the length of the support cable required to support the tower with the floor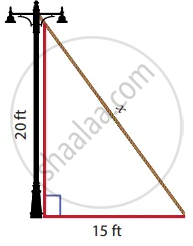
In an isosceles triangle PQR, the length of equal sides PQ and PR is 13 cm and base QR is 10 cm. Find the length of perpendicular bisector drawn from vertex P to side QR.
Two angles are said to be ______, if they have equal measures.
In a triangle, sum of squares of two sides is equal to the square of the third side.
