Advertisements
Advertisements
प्रश्न
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
उत्तर
Correct answer: A
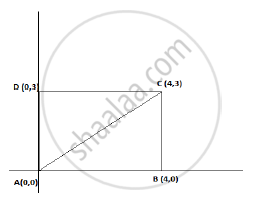
We see that AB = 4 units and BC = 3 units
Using Pythagoras theorem
AC2= AB2+ BC2
=42 + 32
AC 2 =25
Thus AC = 5 units
Hence length of the diagonal of the rectangle is 5 units
APPEARS IN
संबंधित प्रश्न
For finding AB and BC with the help of information given in the figure, complete following activity.
AB = BC .......... 
∴ ∠BAC = 
∴ AB = BC =  × AC
× AC
=  × `sqrt8`
× `sqrt8`
=  × `2sqrt2`
× `2sqrt2`
= 

In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

In the figure: ∠PSQ = 90o, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
Find the length of the perpendicular of a triangle whose base is 5cm and the hypotenuse is 13cm. Also, find its area.
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

The top of a broken tree touches the ground at a distance of 12 m from its base. If the tree is broken at a height of 5 m from the ground then the actual height of the tree is ______.
Two rectangles are congruent, if they have same ______ and ______.
