Advertisements
Advertisements
प्रश्न
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
उत्तर
Correct answer: B
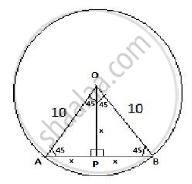
Given ∠ AOB is given as 90º
ΔAOB is an isosceles triangle since OA = OB
Therefore ∠OAB = ∠OBA = 45º
Thus ∠ AOP = 45º and ∠ BOP = 45º
Hence ΔAOP and ΔBOP also are isosceles triangles
AP = OP and OP PB
In ΔAOP
x2 + x2 = 102 [Pythagoras theorem]
Thus 2 x2 = 100
x=5√2
Hence length of chord AB = 2 x = 5√2+5√2=10√2
APPEARS IN
संबंधित प्रश्न
Prove that there is one and only one tangent at any point on the circumference of a circle.
If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
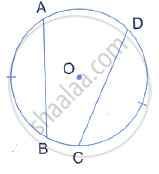
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
The ratio between the circumference and diameter of any circle is _______
If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
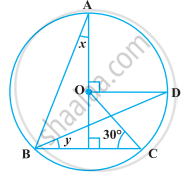
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.