Advertisements
Advertisements
рдкреНрд░рд╢реНрди
If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
рдЙрддреНрддрд░
Given,
PQ = 24 cm
OQ = 25 cm
OP = radius = ?
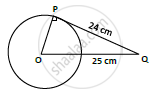
P is point of contact, At point of contact, tangent and radius are perpendicular to each other
∴ ΔPOQ is right angled triangle ∠OPQ = 90°
By Pythagoras theorem,
ЁЭСГЁЭСД2 + ЁЭСВЁЭСГ2 = ЁЭСВЁЭСД2
⇒ 242 + ЁЭСВЁЭСГ2 = 252
⇒`PO = sqrt((25)^2 − (24)^2) = sqrt(625 − 576)`
= `sqrt(49)` = 7ЁЭСРЁЭСЪ
∴ ЁЭСВЁЭСГ = ЁЭСЯЁЭСОЁЭССЁЭСЦЁЭСвЁЭСа = 7ЁЭСРЁЭСЪ
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
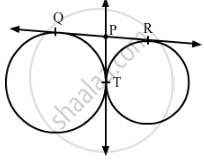
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
