Advertisements
Advertisements
प्रश्न
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
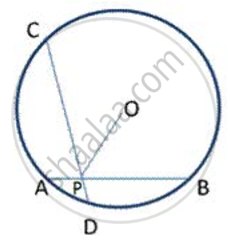
उत्तर
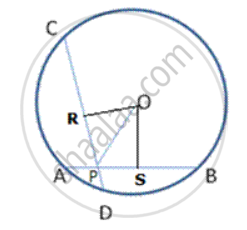
Draw perpendiculars OR and OS to CD and AB respectively.
In triangle ORP and triangle OSP
OP= OP
OR = OS (Distance of equal chords from centre are equal)
∠ PRO = ∠ PSO (right angles)
Therefore, Δ ORP ≅ Δ OSP
Hence, ∠ RPO = ∠ SPO
Thus OP bisects ∠ CPB.
APPEARS IN
संबंधित प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
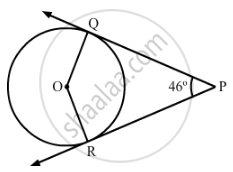
(A) 67°
(B) 134°
(C) 44°
(D) 46°
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is ______.
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
In the given figure, the area enclosed between the two concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c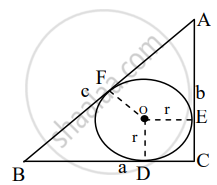
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
