Advertisements
Advertisements
Question
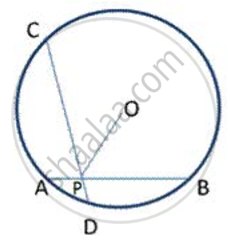
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
Solution
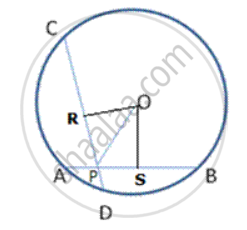
Draw perpendiculars OR and OS to CD and AB respectively.
In triangle ORP and triangle OSP
OP= OP
OR = OS (Distance of equal chords from centre are equal)
∠ PRO = ∠ PSO (right angles)
Therefore, Δ ORP ≅ Δ OSP
Hence, ∠ RPO = ∠ SPO
Thus OP bisects ∠ CPB.
APPEARS IN
RELATED QUESTIONS
In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
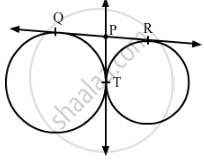
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
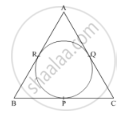
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

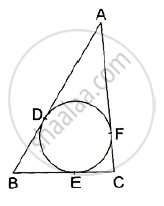
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
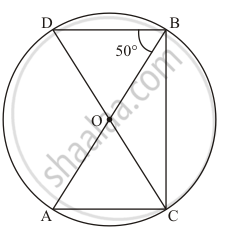
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
In the given figure, if ∠ABC = 45°, then ∠AOC =
Draw circle with the radii given below.
4 cm
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.