Advertisements
Advertisements
Question
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
Solution
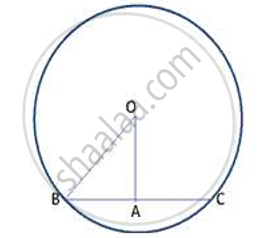
BA = AC ----(1) (Perpendicular from centre to a chord bisects the chord)
In right Δ OAB,
By Pythagoras theorem, OB2 = OA2 + AB2
AB2 = 6.52 + 2.52
= 42.25 - 6.25 = 36
AB = 6cm
∴ Length of chord BC = 2 AB (from (1))
= 2 (6) = 12 cm
APPEARS IN
RELATED QUESTIONS
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA.
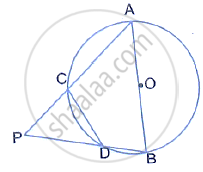
Is AC produced and BD produced meet at point P; show that ∠APB = 60°
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
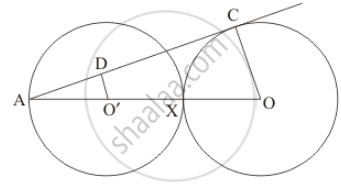
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
Find the area of a circle of radius 7 cm.
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
From the figure, identify a chord.

