Advertisements
Advertisements
Question
Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
Solution
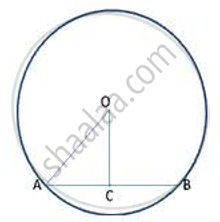
AC = CB ----(1) (Perpendicular from centre to a chord bisects the chord)
In right Δ ACO,
By Pythagoras theorem, OA2 = OC2 + AC2
AC2 = (1. 7)2 - (1.5)2 = 2.89 - 2.25 =.64
AC = 0.8 cm
∴ length of chord AB = 2AC (from ( 1))
= 2(0.8) = 1.6 cm
APPEARS IN
RELATED QUESTIONS
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
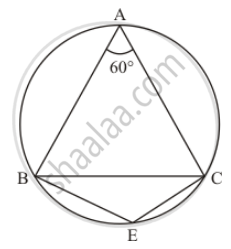
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
Find the diameter of the circle
Radius = 10 cm
A line through the point of contact and passing through centre of the circle is known as ______
