Advertisements
Advertisements
Question
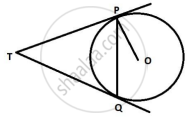
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

Solution
PA and PB are tangents drawn from an external point P to the circle.
∴ PA = PB (Length of tangents drawn from an external point to the circle are equal.)
In ∆PAB,
PA = PB
⇒ ∠PBA = ∠PAB .....(1) (Angles opposite to equal sides are equal.)
Now,
∠APB + ∠PBA + ∠PAB = 180°
⇒ 50º + ∠PAB + ∠PAB = 180° [Using (1)]
⇒ 2∠PAB = 130°
⇒ ∠PAB =`130^@/2`= 65°
We know that radius is perpendicular to the tangent at the point of contact.
∴ ∠OAP = 90° (OA ⊥ PA)
⇒ ∠PAB + ∠OAB = 90°
⇒ 65° + ∠OAB = 90°
⇒∠OAB = 90° − 65° = 25°
Hence, the measure of ∠OAB is 25°.
APPEARS IN
RELATED QUESTIONS
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
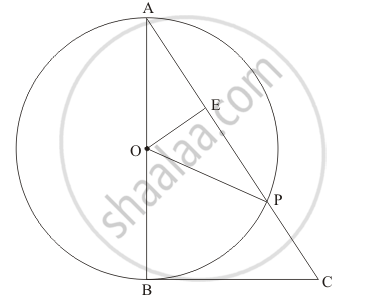
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
From the figure, identify the centre of the circle.