Advertisements
Advertisements
प्रश्न
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

उत्तर
PA and PB are tangents drawn from an external point P to the circle.
∴ PA = PB (Length of tangents drawn from an external point to the circle are equal.)
In ∆PAB,
PA = PB
⇒ ∠PBA = ∠PAB .....(1) (Angles opposite to equal sides are equal.)
Now,
∠APB + ∠PBA + ∠PAB = 180°
⇒ 50º + ∠PAB + ∠PAB = 180° [Using (1)]
⇒ 2∠PAB = 130°
⇒ ∠PAB =`130^@/2`= 65°
We know that radius is perpendicular to the tangent at the point of contact.
∴ ∠OAP = 90° (OA ⊥ PA)
⇒ ∠PAB + ∠OAB = 90°
⇒ 65° + ∠OAB = 90°
⇒∠OAB = 90° − 65° = 25°
Hence, the measure of ∠OAB is 25°.
APPEARS IN
संबंधित प्रश्न
Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at center.
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Draw circle with diameter: 8.4 cm
In above case, measure the length of the radius of the circle drawn.
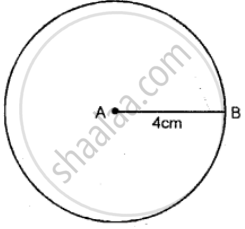
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

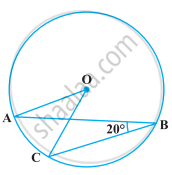
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.
Find the length of the arc of a circle which subtends an angle of 60° at the centre of the circle of radius 42 cm.
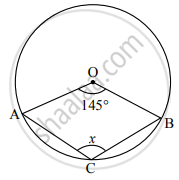
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.