Advertisements
Advertisements
प्रश्न
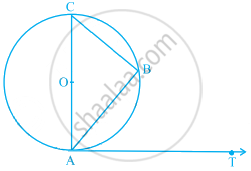
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

उत्तर
We know that the angle subtended by an arc of a circle at the centre is twice the angle subtended by it at any point on the remaining part of the circle.
∴ ∠AOQ = 2∠ABQ
⇒ ∠ABQ =`1/2`∠AOQ
⇒ ∠ABQ =`1/2`×58°=29°
or ∠ABT = 29°
We know that the radius is perpendicular to the tangent at the point of contact.
∴ ∠OAT = 90° (OA ⊥ AT)
or ∠BAT = 90°
Now, in ∆BAT,
∠BAT+∠ABT+∠ATB=180°
⇒90°+29°+∠ATB=180°
⇒∠ATB=180°−119°=61°
∴∠ATQ=61°
APPEARS IN
संबंधित प्रश्न
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
Write True or False. Give reason for your answer.
A circle is a plane figure.
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
The longest chord of a circle is __________
In figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70° and (arc RS) = 80°, find
(i) m(arc PR)
(ii) m(arc QS)
(iii) m(arc QSR)
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
What is the area of a semi-circle of diameter ‘d’?
