Advertisements
Advertisements
प्रश्न
What is the area of a semi-circle of diameter ‘d’?
विकल्प
`1/16 πd^2`
`1/4 πd^2`
`1/8 πd^2`
`1/2 πd^2`
उत्तर
`bb(1/8 πd^2)`
Explanation:
As we know that,
Area of semi-circle = `(πr^2)/2`
and radius (r) = `("Diameter" (d))/2`
∴ r = `d/2`
Thus, area of semi-circle = `π/2(d/2)^2`
= `(πd^2)/(2 xx 4)`
= `(πd^2)/8`
APPEARS IN
संबंधित प्रश्न
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
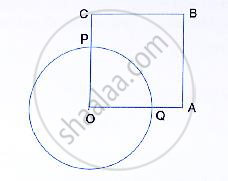
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
If all the sides of a parallelogram touch a circle, show that the parallelogram is a rhombus.
A line segment which joins any two points on a circle is a ___________
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.