Advertisements
Advertisements
Question
What is the area of a semi-circle of diameter ‘d’?
Options
`1/16 πd^2`
`1/4 πd^2`
`1/8 πd^2`
`1/2 πd^2`
Solution
`bb(1/8 πd^2)`
Explanation:
As we know that,
Area of semi-circle = `(πr^2)/2`
and radius (r) = `("Diameter" (d))/2`
∴ r = `d/2`
Thus, area of semi-circle = `π/2(d/2)^2`
= `(πd^2)/(2 xx 4)`
= `(πd^2)/8`
APPEARS IN
RELATED QUESTIONS
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
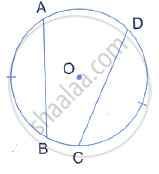
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

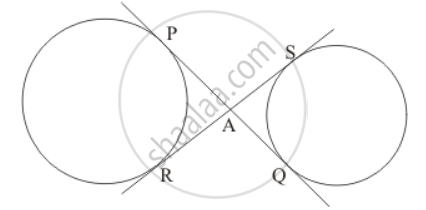
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
The ______________ is the longest chord of a circle
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
In the given figure, O is the centre of the circle. Shade sectors OAC and OPB.