Advertisements
Advertisements
Question
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
Solution

Given: We have a circle whose centre is O and chords AB and AC are equal. AM is the bisector of ∠BAC.
To prove: Centre O lies on the bisector of ∠BAC.
Construction: Join BM and CM.
Proof: In ΔBAM and ΔCAM,
AB = AC ...[Given]
∠BAM = ∠CAM ...[Given]
AM = AM ...[Common]
∴ ΔBAM ≅ ΔCAM ...[By SAS congruency]
`\implies` BM = CM [By C.P.C.T.] ...(i)
And ∠BMA = ∠CMA [By C.P.C.T.] ...(ii)
In ΔBOM and ΔCOM,
BM = CM ...[By (i)]
OM = OM ...[Common]
∠BMO = ∠CMO ...[By (ii)]
∴ ΔBOM and ΔCOM ...[By SAS congruency]
`\implies` ∠BOM = ∠COM [By C.P.C.T.] ...(iii)
Since, ∠BOM + ∠COM = 180° ...(iv)
∴ By (iii) and (iv), ∠BOM = ∠COM = 90°
So, AM is the perpendicular bisector of the chord BC.
Thus, bisector of ∠BAC i.e., AM passes through the centre O.
APPEARS IN
RELATED QUESTIONS
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Draw circle with the radii given below.
3 cm
The ratio between the circumference and diameter of any circle is _______
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c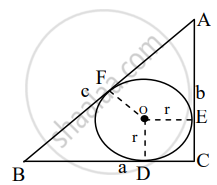
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

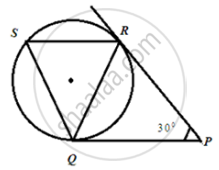
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
