Advertisements
Advertisements
प्रश्न
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
उत्तर

Given: We have a circle whose centre is O and chords AB and AC are equal. AM is the bisector of ∠BAC.
To prove: Centre O lies on the bisector of ∠BAC.
Construction: Join BM and CM.
Proof: In ΔBAM and ΔCAM,
AB = AC ...[Given]
∠BAM = ∠CAM ...[Given]
AM = AM ...[Common]
∴ ΔBAM ≅ ΔCAM ...[By SAS congruency]
`\implies` BM = CM [By C.P.C.T.] ...(i)
And ∠BMA = ∠CMA [By C.P.C.T.] ...(ii)
In ΔBOM and ΔCOM,
BM = CM ...[By (i)]
OM = OM ...[Common]
∠BMO = ∠CMO ...[By (ii)]
∴ ΔBOM and ΔCOM ...[By SAS congruency]
`\implies` ∠BOM = ∠COM [By C.P.C.T.] ...(iii)
Since, ∠BOM + ∠COM = 180° ...(iv)
∴ By (iii) and (iv), ∠BOM = ∠COM = 90°
So, AM is the perpendicular bisector of the chord BC.
Thus, bisector of ∠BAC i.e., AM passes through the centre O.
APPEARS IN
संबंधित प्रश्न
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
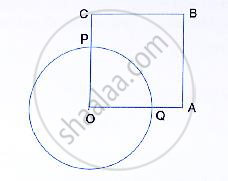
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
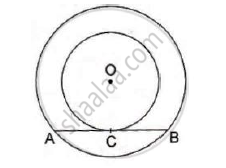
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.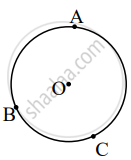
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
