Advertisements
Advertisements
प्रश्न
A, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
उत्तर
Given: A, B and C are three points on a circle.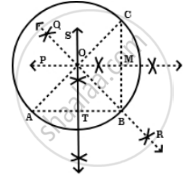
To prove: That perpendicular bisector of AB, BC and CA.
Construction: Draw perpendicular bisectors ST of AB, PM of BC and QR of CA. Join AB, BC and CA.
Proof: OA = OB ...(i) [O lies on ST, the perpendicular bisector of AB]
Again, OB = OC ...(ii) [O lies on PM the perpendicular bisector of BC]
And OC = OA ...(iii) [O lies on QR, the perpendicular bisector of CA]
Now, from equations (i), (ii) and (iii),
OA = OB = OC = r
So, draw a circle with centre O and radius r, that will pass through A, B and C.
That means a circle passing through the point A, B and C. Since, ST, PM or QR can cut each other at one and only one point O.
Therefore, O is the only one point which is equidistance from A, B and C.
Hence, the perpendicular bisector of AB, BC and CA are concurrent.
APPEARS IN
संबंधित प्रश्न
A line segment AB is of length 5 cm. Draw a circle of radius 4 cm passing through A and B. Can you draw a circle of radius 2 cm passing through A and B? Give reason in support of your answer.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. if the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre?
Three girls Ishita, Isha and Nisha are playing a game by standing on a circle of radius 20 m drawn in a park. Ishita throws a ball o Isha, Isha to Nisha and Nisha to Ishita. If the distance between Ishita and Isha and between Isha and Nisha is 24 m each, what is the distance between Ishita and Nisha.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
If the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc PXA ≅ arc PYB.
If BM and CN are the perpendiculars drawn on the sides AC and AB of the triangle ABC, prove that the points B, C, M and N are concyclic.
Two circles with centres O and O′ intersect at two points A and B. A line PQ is drawn parallel to OO′ through A(or B) intersecting the circles at P and Q. Prove that PQ = 2 OO′.
