Advertisements
Advertisements
प्रश्न
Two circles with centres O and O′ intersect at two points A and B. A line PQ is drawn parallel to OO′ through A(or B) intersecting the circles at P and Q. Prove that PQ = 2 OO′.
उत्तर
Firstly draw two circles with center O and O’ such that they intersect at A and B.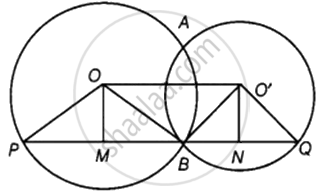
Draw a line PQ parallel to OO’.
In the circle with center O, we have:
OP and OB are the radii of the circle.
PB is the chord with OM as its perpendicular bisector.
i.e. BM = MP ...(1)
In the circle with center O’, we have:
O’B and O’Q are the radii of the circle.
BQ is the chord with O’N as its perpendicular bisector.
i.e. BN = NQ ...(2)
From (1) and (2), we have:
BM + BN = MP + NQ
⇒ (BM + BN) + (BM + BN) = (BM + BN) + (MP + NQ)
⇒ 2(BM + BN) = (BM + BN) + (MP + NQ)
⇒ 2(OO’) = (BM + MP) + (BN + NQ)
⇒ 2(OO’) = BP + BQ
⇒ 2(OO’) = PQ
Hence proved.
APPEARS IN
संबंधित प्रश्न
A line segment AB is of length 5 cm. Draw a circle of radius 4 cm passing through A and B. Can you draw a circle of radius 2 cm passing through A and B? Give reason in support of your answer.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. if the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre?
Three girls Ishita, Isha and Nisha are playing a game by standing on a circle of radius 20 m drawn in a park. Ishita throws a ball o Isha, Isha to Nisha and Nisha to Ishita. If the distance between Ishita and Isha and between Isha and Nisha is 24 m each, what is the distance between Ishita and Nisha.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
If the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc PXA ≅ arc PYB.
A, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
If BM and CN are the perpendiculars drawn on the sides AC and AB of the triangle ABC, prove that the points B, C, M and N are concyclic.
