Advertisements
Advertisements
प्रश्न
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
उत्तर
Draw a quadrilateral ABCD inscribed in a circle having centre O.
Given, ∠ADC = 130°
Since, ABCD is a quadrilateral inscribed in a circle, therefore ABCD becomes a cyclic quadrilateral.
∵ Since, the sum of opposite angles of a cyclic quadrilateral is 180°.
∴ ∠ADC + ∠ABC = 180°
⇒ 130° + ∠ABC = 180°
⇒ ∠ABC = 50°
Since, AB is a diameter of a circle, then AB subtends an angle to the circle is right angle.
∴ ∠ACB = 90°
In ΔABC, ∠BAC + ∠ACB + ∠ABC = 180° ...[By angle sum property of a triangle]
⇒ ∠BAC + 90° + 50° = 180°
⇒ ∠BAC = 180° – (90° + 50°)
= 180° – 140°
= 40°
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
In the given figure, O is the centre of the circle. Find ∠CBD.

AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
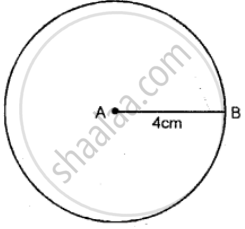
The longest chord of a circle is __________
A line segment joining any point on the circle to its center is called the _____________ of the circle
