Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of the circle. Find ∠CBD.

उत्तर
It is given that, `angle AOC = 100°`
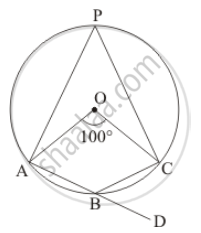
We have to find `angleCBD`
Since `angleAOC = 100°` (Given)
So,
`angleAPC = 1/2 angleAOC` (The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.)
`⇒ angleAPC = 1/2 xx 100`
= 50°
Now,
`angle APC + angleABC = 180° ` (Opposite pair of angle of cyclic quadrilateral)
So,
`50°+ angleABC = 180° `
`angleABC = 180° - 50°`
= 130°
⇒`angle ABC` = 130° …… (1)
`angle ABC + angleCBD = 180° ` (Linear pair)
`130° + angle CBD = 180° ( angleABC = 130)`
`angle CBD = 180° - 130° `
= 50°
Hence `angle CBD ` = 50°
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
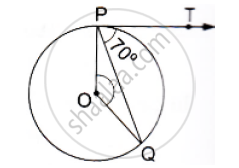
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
Use the figure given below to fill in the blank:
AB is a ______ of the circle.

Twice the radius is ________________
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.
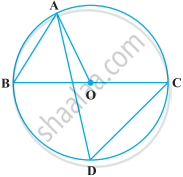
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
