Advertisements
Advertisements
प्रश्न
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

उत्तर
It is given that, ABCD is cyclic quadrilateral in which AD || BC
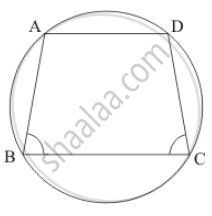
We have to prove `angleB = angle C`
Since, ABCD is a cyclic quadrilateral
So,
`angle B + angle D = 180°` and `angle A + angle C = 180°` ..… (1)
`⇒ angleB + angle A ` = 180° and `angle C + angle D = 180°` (Sum of pair of consecutive interior angles is 180°) …… (2)
From equation (1) and (2) we have
`angleB + angleD + angleB + angle A ` = 360° …… (3)
`angleA + angleC + angleC + angle D ` = 360° …… (4)
`2angleB + angleD + angleA = 2 angleC + angleA + angleD`
`2angleB = 2angleC`
`angleB = angleC`
Hence Proved
APPEARS IN
संबंधित प्रश्न
PA and PB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
The ______________ is the longest chord of a circle
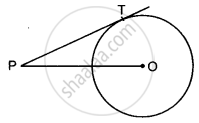
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]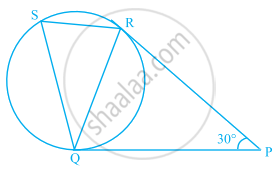
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
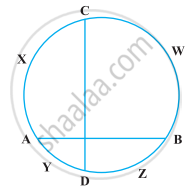
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.
What is the area of a semi-circle of diameter ‘d’?
