Advertisements
Advertisements
प्रश्न
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
उत्तर
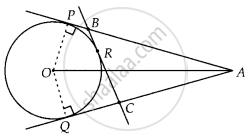
OP ⊥ AP
∴ ∠OPA = 90° ...[Tangent at any point of a circle is perpendicular to the radius through the point of contact]
In ∆OAP,
OA2 = OP2 + PA2
⇒ 132 = 52 + PA2
⇒ PA = 12 cm
Now, perimeter of ∆ABC = AB + BC + CA
= AB + BR + RC + CA
= (AB + BR) + (RC + CA)
= (AB + BP) + (CQ + CA) ...[∵ BR = BP, RC = CQ i.e., tangents from external point to a circle are equal]
= AP + AQ
= 2AP ...[∵ AP = AQ]
= 2 × 12
= 24 cm
Hence, the perimeter of ∆ABC = 24 cm.
संबंधित प्रश्न
In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
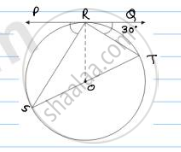
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
true or false
The degree measure of an arc is the complement of the central angle containing the arc.
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
The point of concurrence of all angle bisectors of a triangle is called the ______.
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.
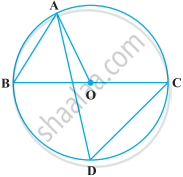
From the figure, identify a chord.

Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
