Advertisements
Advertisements
प्रश्न
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
उत्तर
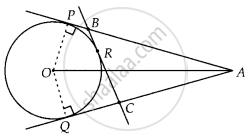
OP ⊥ AP
∴ ∠OPA = 90° ...[Tangent at any point of a circle is perpendicular to the radius through the point of contact]
In ∆OAP,
OA2 = OP2 + PA2
⇒ 132 = 52 + PA2
⇒ PA = 12 cm
Now, perimeter of ∆ABC = AB + BC + CA
= AB + BR + RC + CA
= (AB + BR) + (RC + CA)
= (AB + BP) + (CQ + CA) ...[∵ BR = BP, RC = CQ i.e., tangents from external point to a circle are equal]
= AP + AQ
= 2AP ...[∵ AP = AQ]
= 2 × 12
= 24 cm
Hence, the perimeter of ∆ABC = 24 cm.
संबंधित प्रश्न
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

Write True or False. Give reason for your answer.
A circle is a plane figure.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

In the given figure, if ∠ABC = 45°, then ∠AOC =
Draw a circle of radius 4.8 cm and mark its center as P.
(i) Draw radii PA and PB such that ∠APB = 45°.
(ii) Shade the major sector of the circle
The longest chord of a circle is __________
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).

Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c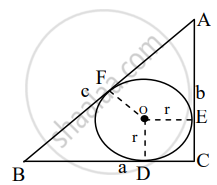
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.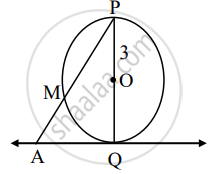
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
