Advertisements
Advertisements
प्रश्न
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

उत्तर
We have to prove that
AQ = `1/2` (perimeter of ΔABC)
Perimeter of ΔABC = AB + BC + CA
= AB + BP + PC + CA
= AB + BQ + CR + CA
(∵ Length of tangents from an external point to a circle are equal ∴ BP = BQ and PC = CR)
= AQ + AR ...(∵ AB + BQ = AQ and CR + CA = AR)
= AQ + AQ ...(∵ Length of tangents from an external point are equal)
= 2AQ
`\implies` AQ = `1/2` (Perimeter of ΔABC)
Hence proved.
संबंधित प्रश्न
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
Draw circle with diameter: 8.4 cm
In above case, measure the length of the radius of the circle drawn.
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
Find the radius of the circle
Diameter = 24 cm
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.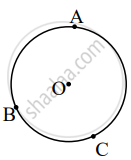
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.