Advertisements
Advertisements
प्रश्न
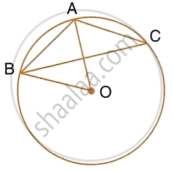
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

उत्तर
Given: ∠AOB = 90°, ∠ABC = 30°
To find: ∠CAB
Solution:
In given figure,
∠AOB = m (arc AB) ......[Definition of measure of minor arc]
∴ m(arc AB) = 90° ......(i)
Also, ∠ACB = `1/2` m(arc AB) .....[Inscribed angle theorem]
∴ ∠ACB = `1/2 xx 90^circ` ......[From (i)]
∴ ∠ACB = 45° .....(ii)
In ∆ACB,
∠CAB + ∠ABC + ∠ACB = 180° ......`[("Sum of the measures of"),("angles of a triangle is" 180^circ)]`
∴ ∠CAB + 30° + 45° = 180° ......[From (ii)]
∴ ∠CAB + 75° = 180°
∴ ∠CAB = 180° – 75°
∠CAB = 105°
संबंधित प्रश्न
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
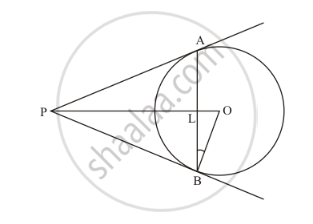
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
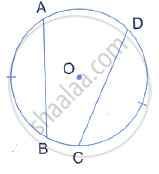
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
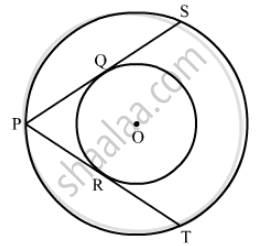
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
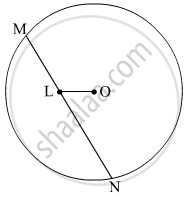
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
Use the figure given below to fill in the blank:
EF is a ______ of the circle.

Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
In the table below, write the names of the points in the interior and exterior of the circle and those on the circle.
| Diagram | Points in the interior of the circle |
Points in the exterior of the circle |
Points on the circle |
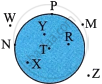 |
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
Twice the radius is ________________
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
From the figure, identify three radii.