Advertisements
Advertisements
प्रश्न
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.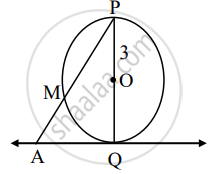
उत्तर
Given: line AQ is a tangent.
OP = 3, m(arc PM) = 120°
To find: AP
In the given figure, arc PMQ is a semicircle.
∴ m(arc PMQ) = 180° ......[Measure of semicircular arc is 180°]
∴ m(arc PM) + m(arc MQ) = 180° .....[Arc addition property]
∴ 120° + m(arc MQ) = 180° ......[Given]
∴ m(arc MQ) = 180° – 120°
∴ m(arc MQ) = 60° .......(i)
∠MPQ = `1/2` m(arc MQ) .....[Inscribed angle theorem]
∴ ∠MPQ = `1/2 xx 60^circ` ......[From (i)]
∴ ∠MPQ = 30°
i.e., ∠APQ = 30° ......(ii) [A – M – P]
In ∆PQA, ∠PQA = 90° ......[Tangent theorem]
∠ APQ = 30° ......[From (ii)]
∴ ∠PAQ = 60° ......[Remaning angle of ∆PQA]
∴ ∆PAQ is 30° – 60° – 90° triangle.
∴ PQ = `sqrt(3)/2` AP ......[Side opposite to 60°]
∴ (PO + OQ) = `sqrt(3)/2` AP ......[P – O – Q]
∴ (3 + 3) = `sqrt(3)/2` AP ......[Radii of same circle and op = 3]
∴ AP = `(6 xx 2)/sqrt(3)`
∴ AP = `(6 xx 2 xx sqrt(3))/(sqrt(3) xx sqrt(3))` ......[Multiply and divide by `sqrt(3)`]
∴ AP = `(6 xx 2 xx sqrt(3))/3`
∴ AP = `2 xx 2sqrt(3)`
∴ AP = `4sqrt(3)` units
APPEARS IN
संबंधित प्रश्न
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
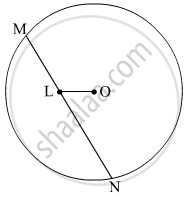
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
From the figure, identify a chord.

From the figure, identify a point in the exterior.

From the figure, identify a segment.

Say true or false:
The centre of a circle is always in its interior.
