Advertisements
Advertisements
प्रश्न

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
उत्तर
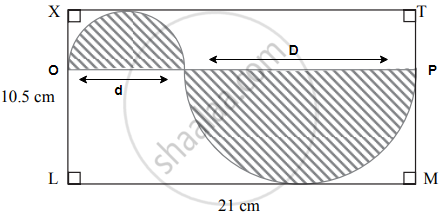
Given: `square`XLMT is a rectangle.
LM = XT and XL = TM .....(Opposite sides are equal)
∴ XT = 21 cm
TM = 10.5 cm
To find the area of a non-shaded region
The diameter of a smaller semicircle is half the diameter of a larger semi-circle.
Let the diameter of the larger semicircle is D and the diameter of the smaller semicircle be `1/2 xx D = D/2`.
Now, the diameter of the smaller semicircle + the diameter of the larger semicircle = 21 cm
`D + D/2 = 21`
`(2D + D)/2 = 21`
`(3D)/2 = 21`
`3D = 21 xx 2`
`D = (21 xx 2)/3`
D = 14
A(smaller semi-circle) = `1/2 pir^2`
= `1/2 xx 22/7 xx 7/2 xx 7/2`
= `77/4 "cm"^2`
A(largerer semi-circle) = `1/2pir^2`
`= 1/2 xx 22/7 xx 14/2 xx 14/2`
= `77 "cm"^2`
A(`square`XLMT) = length × breadth
= LM × XL
= 21 cm × 10.5 cm
= 220.5 cm2
Area of the non-shaded region
= A(`square`XLMT) – A(smaller semi-circle) – A(larger semi-circle)
= 220.5 – `77/4 - 77`
= 220.5 – 19.25 – 77
= 124.25 cm2
APPEARS IN
संबंधित प्रश्न
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

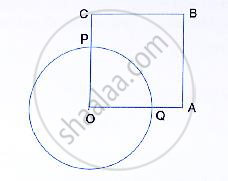
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
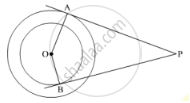
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
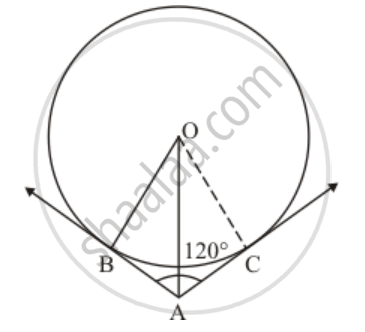
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
The point of concurrence of all angle bisectors of a triangle is called the ______.
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

Two concentric circles with center O have A, B, C, D as the points of intersection with the lines L shown in the figure. If AD = 12 cm and BC s = 8 cm, find the lengths of AB, CD, AC and BD.
Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm. Draw the incircle of the triangle ABC.
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
Find the radius of the circle
Diameter = 30 cm
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
