Advertisements
Advertisements
प्रश्न
Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
उत्तर
AB is the diameter of circle
i.e. AB = 6 cm
and OA is the radius of circle

`= 1/2 "of diameter" = 6/2 = 3` cm
i.e., OA = OB = 3 cm.
APPEARS IN
संबंधित प्रश्न
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
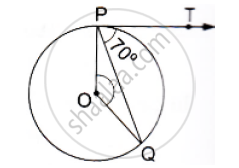
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
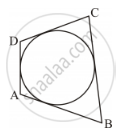
In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

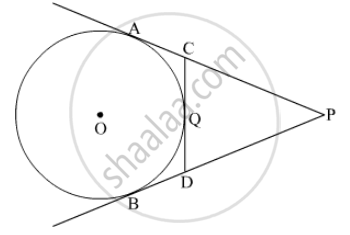
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.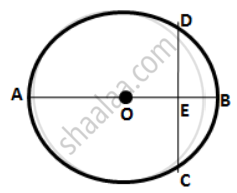
A line segment with its end points on the circle is called a ______________
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
