Advertisements
Advertisements
प्रश्न
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
उत्तर
et XBY and PCQ be two parallel tangents to a circle with centre O.
Construction: Join OB and OC.
Draw OA∥XY
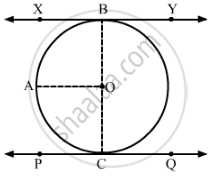
Now, XB∥AO
⇒ ∠XBO + ∠AOB = 180° (sum of adjacent interior angles is 180°)
Now, ∠XBO = 90° (A tangent to a circle is perpendicular to the radius through the point of contact)
⇒ 90° + ∠AOB = 180°
⇒ ∠AOB = 180° − 90° = 90°
Similarly, ∠AOC = 90°
∴ ∠AOB + ∠AOC = 90° + 90° = 180°
Hence, BOC is a straight line passing through O.
Thus, the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
APPEARS IN
संबंधित प्रश्न
Fill in the blank
The angle between tangent at a point on a circle and the radius through the point is ........
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
true or false
A circle is a plane figure.
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

A circle of radius 3 cm can be drawn through two points A, B such that AB = 6 cm.
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
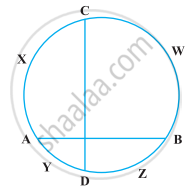
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.