Advertisements
Advertisements
प्रश्न
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

उत्तर
It is given that, ABCD is cyclic quadrilateral in which AD || BC
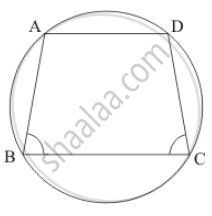
We have to prove `angleB = angle C`
Since, ABCD is a cyclic quadrilateral
So,
`angle B + angle D = 180°` and `angle A + angle C = 180°` ..… (1)
`⇒ angleB + angle A ` = 180° and `angle C + angle D = 180°` (Sum of pair of consecutive interior angles is 180°) …… (2)
From equation (1) and (2) we have
`angleB + angleD + angleB + angle A ` = 360° …… (3)
`angleA + angleC + angleC + angle D ` = 360° …… (4)
`2angleB + angleD + angleA = 2 angleC + angleA + angleD`
`2angleB = 2angleC`
`angleB = angleC`
Hence Proved
APPEARS IN
संबंधित प्रश्न
If the tangent at point P to the circle with center O cuts a line through O at Q such that PQ= 24cm and OQ = 25 cm. Find the radius of circle
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

Use the figure given below to fill in the blank:
Tangent to a circle is _______.

The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
The longest chord of a circle is __________
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
