Advertisements
Advertisements
प्रश्न
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

उत्तर
It is given that ∠BCD = 100° and ∠ABD = 70°
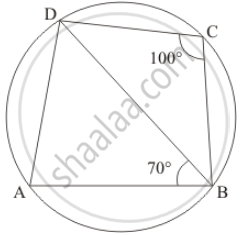
We have to find the ∠ADB
We have
∠A + ∠C = 180° (Opposite pair of angle of cyclic quadrilateral)
So,
`angle A = 180° - 100°`
= 80°
Now in Δ ADB is `angle A ` = 80° and `angle ABD` = 70°
Therefore,
`angle A + angle ADB + angle ABD = 180°`
`80° + angleADB + 70° = 180°`
`angleADB = 180° - 150°`
= 30°
Hence, `angleADB` = 30°
APPEARS IN
संबंधित प्रश्न
Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
true or false
A circle is a plane figure.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
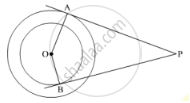
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
If O is the centre of the circle, find the value of x in each of the following figures
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
