Advertisements
Advertisements
प्रश्न
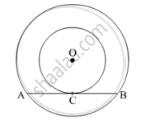
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
उत्तर
Given: Two concentric circles C1 and C2 with centre O, and AB is the chord of C1 touching C2 at C.
To prove: AC = CB
Construction: Join OC.
Proof: AB is the chord of C1 touching C2 at C, then AB is the tangent to C2 at C with OC as its radius.
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ OC ⊥ AB
Considering, AB as the chord of the circle C1. So, OC ⊥ AB.
∴ OC is the bisector of the chord AB.
Hence, AC = CB (Perpendicular from the centre to the chord bisects the chord).
APPEARS IN
संबंधित प्रश्न
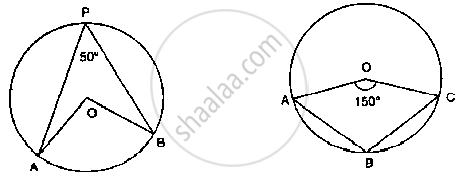
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
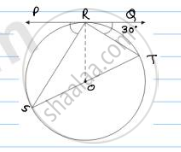
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is ______.
Use the figure given below to fill in the blank:
________ is a radius of the circle.
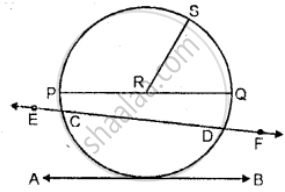
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
If A, B, C and D are four points such that ∠BAC = 45° and ∠BDC = 45°, then A, B, C, D are concyclic.
