Advertisements
Advertisements
प्रश्न
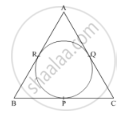
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
उत्तर
Given: An isosceles ΔABC with AB = AC, circumscribing a circle.
To prove: P bisects BC
Proof: AR and AQ are the tangents drawn from an external point A to the circle.
∴ AR = AQ (Tangents drawn from an external point to the circle are equal)
Similarly, BR = BP and CP = CQ.
It is given that in ΔABC, AB = AC.
⇒ AR + RB = AQ + QC
⇒ BR = QC (As AR = AQ)
⇒ BP = CP (As BR = BP and CP = CQ)
⇒ P bisects BC
Hence, the result is proved.
APPEARS IN
संबंधित प्रश्न
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

Write True or False. Give reason for your answer.
A circle is a plane figure.
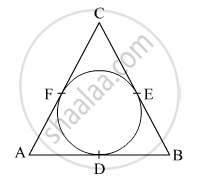
In Fig. 4, a circle inscribed in triangle ABC touches its sides AB, BC and AC at points D, E and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF.
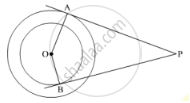
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
In the given figure, the area enclosed between the two concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
From the figure, identify a chord.

