Advertisements
Advertisements
प्रश्न
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
उत्तर
Radius of a circle (OA) = 15 cm
Distance from centre to the chord (OC) = 12 cm
In the right ΔOAC,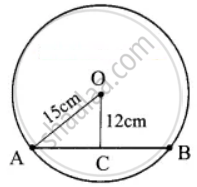
AC2 = OA2 – OC2
= 152 – 122
= 225 – 144
= 81
AC = `sqrt(81)`
= 9
Length of the chord (AB)
= AC + CB
= 9 + 9
= 18 cm.
APPEARS IN
संबंधित प्रश्न
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

One chord of a circle is known to be 10 cm. The radius of this circle must be
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

State, if the following statement is true or false:
The longest chord of a circle is its diameter.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

