Advertisements
Advertisements
प्रश्न
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
उत्तर
Radius of a circle = `4sqrt(2)` cm
In the right ΔAOC,

AC2 = OA2 + OC2
AC2 = `(4sqrt(2))^2 + (4sqrt(2))^2`
= 32 + 32 = 64
AC = `sqrt(64)`
= 8
Length of the chord = 8 cm,
∠OAC = ∠OCA = 45°
Since OAC is an isosceles right angle triangle.
APPEARS IN
संबंधित प्रश्न
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
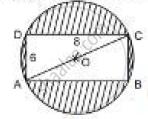
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

Draw circle with diameter: 8.4 cm
In above case, measure the length of the radius of the circle drawn.
Draw circle with the radii given below.
3 cm
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
