Advertisements
Advertisements
प्रश्न
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
उत्तर
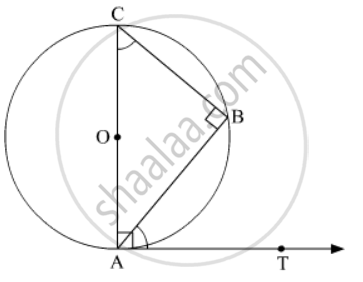
In the given figure,
AC is the diameter.
So,
AT is the tangent at point A.
Thus,
\[ \Rightarrow \angle BCA + 90^o + \angle CAT - \angle BAT = 180^o \]
\[ \Rightarrow \angle BCA + 90^o + 90 - \angle BAT = 180^o \]
\[ \Rightarrow \angle BCA = \angle BAT\]
Hence Proved
APPEARS IN
संबंधित प्रश्न
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
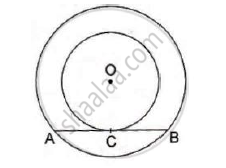
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
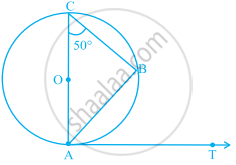
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
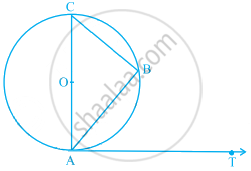
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
In the given figure, O is the centre of the circle. Name a chord, which is not the diameter of the circle.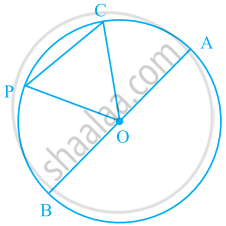
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
