Advertisements
Advertisements
प्रश्न
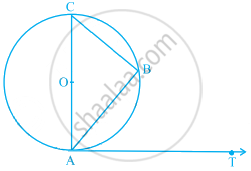
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
उत्तर
Since, AC is a diameter line, so angle in semi-circle an angle 90°.
∴ ∠ABC = 90° ...[By property]
In ∆ABC,
∠CAB + ∠ABC + ∠ACB = 180° ...[∵ Sum of all interior angles of any triangle is 180°]
⇒ ∠CAB + ∠ACB = 180° – 90° = 90° ...(i)
Since, diameter of a circle is perpendicular to the tangent.
i.e., CA ⊥ AT
∴ ∠CAT = 90°
⇒ ∠CAB + ∠BAT = 90° ...(ii)
From equations (i) and (ii),
∠CAB + ∠ACB = ∠CAB + ∠BAT
⇒ ∠ACB = ∠BAT
Hence proved.
APPEARS IN
संबंधित प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
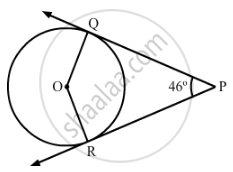
(A) 67°
(B) 134°
(C) 44°
(D) 46°
ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
Fill in the blank
A continuous piece of a circle is ............... of the circle
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

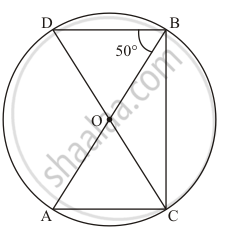
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
Use the figure given below to fill in the blank:
________ is a radius of the circle.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
