Advertisements
Advertisements
Question
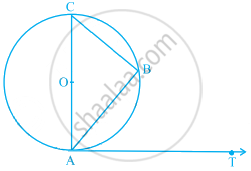
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
Solution
Since, AC is a diameter line, so angle in semi-circle an angle 90°.
∴ ∠ABC = 90° ...[By property]
In ∆ABC,
∠CAB + ∠ABC + ∠ACB = 180° ...[∵ Sum of all interior angles of any triangle is 180°]
⇒ ∠CAB + ∠ACB = 180° – 90° = 90° ...(i)
Since, diameter of a circle is perpendicular to the tangent.
i.e., CA ⊥ AT
∴ ∠CAT = 90°
⇒ ∠CAB + ∠BAT = 90° ...(ii)
From equations (i) and (ii),
∠CAB + ∠ACB = ∠CAB + ∠BAT
⇒ ∠ACB = ∠BAT
Hence proved.
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
Draw a circle of radius 4.8 cm and mark its center as P.
(i) Draw radii PA and PB such that ∠APB = 45°.
(ii) Shade the major sector of the circle
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
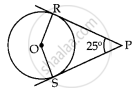
In the given figure, if ZRPS = 25°, the value of ZROS is ______
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
From the figure, identify a segment.

