Advertisements
Advertisements
Question
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
Solution
PA = 14 cm
Perimeter of ΔPCD = PC + PD + CD = PC + PD + CE + ED
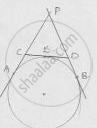
We know that
The two tangents drawn from external point to the circle are equal in length.
From point P, PA = PB = 14cm
From point C, CE = CA
From point D, DB = ED
Perimeter = PC + PD + CA +DB
= (PC + CA) + (PD + DB)
= PA + PB = 14 + 14 = 28 cm.
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

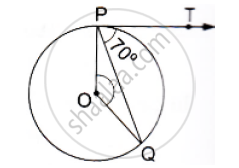
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

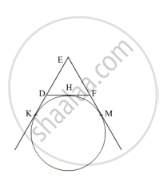
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie.
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
A line through the point of contact and passing through centre of the circle is known as ______
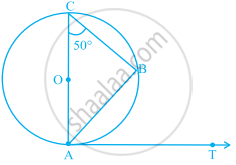
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
From the figure, identify two points in the interior.

