Advertisements
Advertisements
Question
From the figure, identify two points in the interior.

Solution
Two points in the interior - O, P
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

Use the figure given below to fill in the blank:
If the length of RS is 5 cm, the length of PQ = _______

Draw circle with the radii given below.
4 cm
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD.
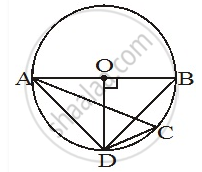
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
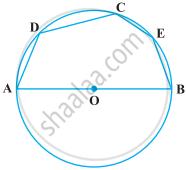
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
