Advertisements
Advertisements
Question
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

Solution
Given: ∠POR = 130°
So, ∠TSR = \[\frac{1}{2}\angle POR = \frac{1}{2} \times 130^o = 65^o = \angle2\] (Since angle subtended by the arc at the centre is double the angle subtended by it at the remaining part of the circle)
∠POQ = 180º − ∠POR = 180º − 130º = 50º .....(2) (Linear pair)
In
Δ POQ, \[\angle1 + \angle POQ + \angle OQP = 180^o\]
\[ \Rightarrow \angle1 + 50^o + 90^o = 180^o\]
\[ \Rightarrow \angle1 = 40^o\]
\[\angle1 + \angle POQ + \angle OQP = 180^o\]
\[ \Rightarrow \angle1 + 50^o + 90^o = 180^o\]
\[ \Rightarrow \angle1 = 40^o\]
\[Now \angle1 + \angle2 = 40^o + 65^o = 105^o\]
APPEARS IN
RELATED QUESTIONS
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
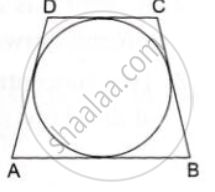
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
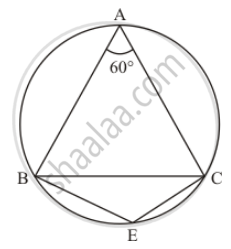
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Draw circle with the radii given below.
3 cm
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 24 m |
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
