Advertisements
Advertisements
Question
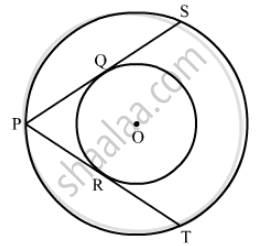
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
Solution
Given that PR = 5 cm.
PR and PQ are the tangents to the inner circle so,
PR = PQ = 5 cm (Tangents drawn from an external point to the circle are equal)
Now draw a perpendicular from the centre O to the tangent PS.
PS is the chord of the inner circle. we know that the perpendicular drawn
from the centre of the circle to the chord bisects the chord. So, PQ = QS = 5 cm
PS = PQ + QS = 5 cm + 5 cm = 10 cm
APPEARS IN
RELATED QUESTIONS
Write True or False. Give reason for your answer.
A circle is a plane figure.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
Use the figure given below to fill in the blank:
Diameter = 2 x ________

Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
State, if the following statement is true or false:
The diameters of a circle always pass through the same point in the circle.
In the table below, write the names of the points in the interior and exterior of the circle and those on the circle.
| Diagram | Points in the interior of the circle |
Points in the exterior of the circle |
Points on the circle |
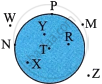 |
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.