Advertisements
Advertisements
Question
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
Options
25 cm
20 cm
40 cm
18 cm
Solution
40 cm
Explanation;
Hint: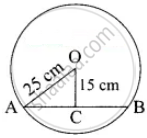
In the right triangle OAC,
AC2 = OA2 – OC2
= 252 – 152
= (25 + 15)(25 – 15)
= 40 × 10
AC2 = 400
AC = `sqrt(400)`
= 20
Length of the chord AB = 20 + 20 = 40 cm.
APPEARS IN
RELATED QUESTIONS
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
In the following figure, AB is the diameter of a circle with centre O and CD is the chord with length equal to radius OA.
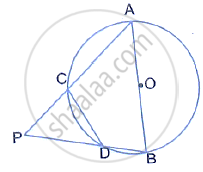
Is AC produced and BD produced meet at point P; show that ∠APB = 60°
An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
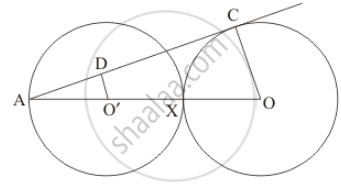
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
Draw circle with the radii given below.
2 cm
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?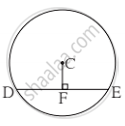
If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
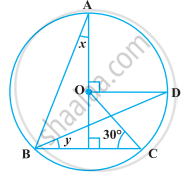
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.