Advertisements
Advertisements
Question
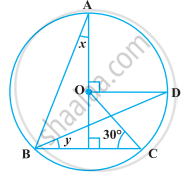
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
Solution
Given, O is the centre of the circle and ∠BCO = 30°. In the given figure join OB and AC.
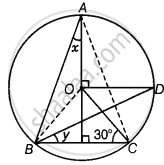
In ΔBOC, CO = BO ...[Both are the radius of circle]
∴ ∠OBC = ∠OCB = 30° ...[Angles opposite to equal sides are equal]
∴ ∠BOC = 180° – (∠OBC + ∠OCE) ...[By angle sum property of a triangle]
= 180° – (30° + 30°)
= 120°
∠BOC = 2∠BAC
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
∴ `∠BAC = 120^circ/2 = 60^circ`
Also, ∠BAE = ∠CAE = 30° ...[AE is an angle bisector of angle A]
⇒ ∠BAE = x = 30°
In ΔABE, ∠BAE + ∠EBA + ∠AEB = 180° ...[By angle sum property of a triangle]
⇒ 30° + ∠EBA + 90° = 180°
∴ ∠EBA = 180° – (90° + 30°)
= 180° – 120°
= 60°
Now, ∠EBA = 60°
⇒ ∠ABD + y = 60°
⇒ `1/2 xx ∠AOD + y = 60^circ` ...[In a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle]
⇒ `90^circ/2 + y = 60^circ` ...[∵ ∠AOD = 90°, given]
⇒ 45° + y = 60°
⇒ y = 60° – 45°
∴ y = 15°
APPEARS IN
RELATED QUESTIONS
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
Use the figure given below to fill in the blank:
______ is a chord of the circle.

In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is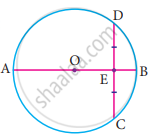
The length of tangent from an external point on a circle is always greater than the radius of the circle.
From the figure, identify the centre of the circle.